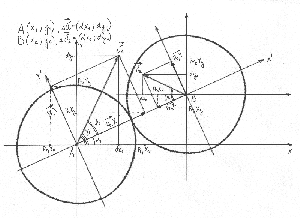
Модель соударения двух бильярдных шаров.
Однажды мне вдруг захотелось самому написать игру. И почему-то именно бильярд. Может быть потому, что эта игра мне всегда нравилась своей непонятной притягательностью… Самому формулы выводить почему-то не хотелось. Поэтому я сразу же полез в интернет и стал искать «математическую модель соударения двух шаров». Как только я не изменял запрос и параметры поиска! В ответ любой поисковик выдавал мне всякую чушь и какие-то философские рассуждения, а также форумы, где были такие же несчастные, как и я. Тогда я решил всё-таки довести это дело до конца и стал выводить формулы.
Поскольку имеются нуждающиеся в нижеприведённых формулах (у кого-то нелады с геометрией, а кому-то, может, просто лень - неважно), то данная статья именно для них.
Я также предоставляю исходники бильярда, реализованной в Delphi пятой версии. Данная программа работает с канвой. Есть также реализация с применением OpenGL.
Кстати, если изменить
немного файл settings.ini, можно получать интересные вещи, например, можно
смоделировать броуновское движение, если шаров будет много, а коэффициент
трения Friction близок к 1 (но не
равен ей!).
Exe-файл работоспособной
программы находится здесь.
Итак, приступим…
Пусть нам известны:
-
координаты центров шаров
-
векторы скоростей
-
радиус шаров R
Нам нужно найти векторы скоростей шаров после соударения
![]()
![]()
Решение
![]()
![]()
![]()
для первого шара:
![]()
![]() ,
, ![]()
![]() , иначе
, иначе
![]()
![]() ,
, ![]()
![]() , иначе
, иначе
![]()
![]()
![]()
![]()
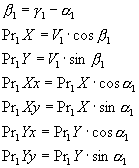
повторяем те же вычисления
для второго шара:
![]()
![]() ,
, ![]()
![]() , иначе
, иначе
![]()
![]() ,
, ![]()
![]() , иначе
, иначе
![]()
![]()
![]()
![]()
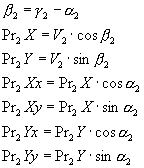
вычисляем составляющие
новых векторов скорости после соударения шаров
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
где ![]() - коэффициент трения,
- коэффициент трения,
![]() <1; например,
<1; например, ![]() =0,97
=0,97
Заметим, однако, что
![]()